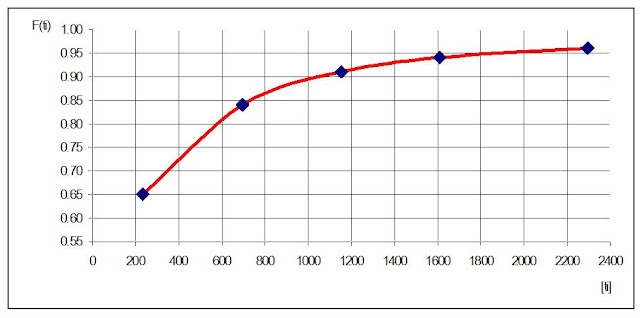
 |
| Figura. Curva de probabilidad de fallo (infiabilidad) de la cernidora crítica. [Fuente: Radical Management. Caso real]. |
LA CONFIABILIDAD de una máquina ─considerando tanto la intrínseca, establecida por diseño; como la operacional, aquella que se logra en el contexto de operación real─ es un atributo determinante para su operatividad, disponibilidad y sus costos de mantenimiento.
Se llega a un momento donde los constantes y prolongados estados de avería
, indican un incremento de la infiabilidad y una baja mantenibilidad no tolerable. Se piensa entonces que es el momento de "invertir" en una nueva máquina o hacer una reparación capital y/o modificaciones a la vieja. ¿Estaremos en lo cierto?
La cernidora que tomaremos de ejemplo, pertenece a un molino de harina. Es una máquina que presenta un registro aceptablemente organizado de la mayor parte de sus estados de avería, si bien se descubrió que no todos los fallos se registraron durante el período de análisis, que fue de dos años.
Después de trabajar con los tiempos entre fallos —realizar ciertas suposiciones y tratar de encontrar un ajuste adecuado a una distribución determinada y aplicando los métodos estadísticos de bondad de ajuste, según el criterio de Kolmogorov-Smirnov, con un grado de calidad en el ajuste de 85%— se verifica atendible el ajuste para la distribución de Weibull, desechando otras posibles hipótesis de distribuciones de fallos (como la exponencial y otras consideradas, debido a su peor calidad en el ajuste para las características de estos datos).
La cernidora es una máquina de baja fiabilidad, ya que cuando transcurre un tiempo medio de aproximadamente nueve días, la misma tiene una probabilidad del 65% de fallar en operación, considerando una exigencia de operación de tres turnos diarios (24 h). Según puede observarse en el despliegue gráfico de la función de infiabilidad obtenida [F(t)], en menos de 3 meses de trabajo la probabilidad de fallo supera el 95%. Ver la figura.
 |
| Figura. Curva de infiabilidad de la cernidora, una máquina crítica. |
Conociendo que la función fiabilidad, R(t), se puede definir como en la fórmula:
Entonces es fácil obtenerla y graficarla una vez que ya se tiene a F(t). Invitamos al lector a que construya la gráfica pertinente.
⚠En este caso, podría cometerse el error tentador de pensar que la indisponibilidad es el resultado de la infiabilidad y, de este modo, omitir que en realidad la situación se debe a problemas con la mantenibilidad.
Esta conclusión, es posible verificarla una vez se conozca el grado de verdad con el que se realiza el proceso de mantener las funciones de la máquina. Para el caso, estaba sometida a una política estrictamente correctiva, aun siendo considerada una máquina crítica, y los estados finales después de las correcciones se debatían generalmente entre: mejor que antes de fallar pero peor que nuevo y tan malo como antes de fallar, lo cual fue acumulando el potencial de infiabilidad descrito.
Se trata de un caso donde se evidencia claramente la relación y el compromiso entre mantenibilidad y confiabilidad. En este caso particularmente se resalta a la confiabilidad operacional como una función de la mantenibilidad lograda en práctica. Asunto que no siempre resulta sencillo demostrar, ya que para algunos es mejor, y más conveniente, justificar las calamidades acusando de “falta de confiabilidad” a los sistemas, cuando tal situación no se verifica como la causa esencial en todos los casos. 🔼
Gracias Estimado Luis F. Sexto, por explicar y compartir de forma sencilla éste caso práctico. Saludos cordiales!
ResponderEliminarAgradecido de su comentario.
EliminarEstimado Luis, en la simplicidad esta la belleza de todo. Aquí valdría la pena poner un granito de arena adicional, y es tratar de cambiar un poco la mentalidad que tenemos, la razón del mantenedor es que el equipo siempre este disponible, entonces me surge la inquietud, si esto es así, porque razón seguimos haciendo evaluaciones de criticidad de equipos en lugar de hacer evaluaciones de mantenibilidad. si bien es cierto, de acuerdo con la teoría equipo critico aquel con muchas fallas o muchas consecuencias, pero porque medir lo negativo en lugar de medir lo positivo; en otras palabras, midamos el tiempo de respuesta de la organización de mantenimiento ante las fallas. Un equipo siempre tendra fallas, pero el tiempo que dure averiado depende de la organización y su nivel de madurez.
ResponderEliminarCordial saludo, no aparece su nombre, por ello no lo puedo mencionar. Pero si responder. Con respecto a las interrogantes del comentario, pues considero que el análisis de criticidad no es otra cosa que un análisis de riesgo, y entre sus variables de análisis debería considerar la mantenibilidad también (junto al impacto a la producción, la calidad, la seguridad, el prestigio, los costos...). Este análisis, entre sus razones tendría el de poder establecer un código para establecer las prioridades en las intervenciones de mantenimiento y una base para la creación de acciones preventivas en función de la criticidad obtenida. Lo que sucede es que en muchas ocaciones la mantenibilidad no la consideran entre las variables de la criticidad. Pero, claro está, en esto el análisis de criticidad no es el responsable...
EliminarBuenos días Luis Felipe, soy Guillermo Díaz, no se si me recordarás.
ResponderEliminarMe gusta tu artículo muchísimo por la síntesis tan buena que haces y el estudio que en este caso es muy corto en el tiempo gracias a la gran cantidad de averías del equipo analizado. Sobre todo me gusta esta frase: "En este caso, podría cometerse el error tentador de pensar que la indisponibilidad es el resultado de la infiabilidad y, de este modo, omitir que en realidad la situación se debe a problemas con la mantenibilidad. ". En mi humilde opinión, esto ocurre por que no se suele introducir la mantenibilidad como un elemento en el cálculo de la criticidad, con lo que a veces se falla estrepitosamente en la adquisición del equipo o en la estrategia de mantenimiento que se le aplica.